参考原文：差分进化算法

一、差分进化算法（DE）原理

差分进化算法同其它进化算法一样（尤其和遗传算法，具有很强的相似性），差分进化算法，也是对候选解的种群进行操作，具体地说，它包含了三个主要的操作：

变异：通过把种群中两个成员之间的加权差向量加到第三个成员上来产生新的参数向量，该操作称为“变异”；
交叉：将变异向量的参数与另外预先确定的目标向量参数按照一定的规则混合来产生试验向量。
选择：如果试验向量的目标函数比目标向量的代价函数低，那么就利用试验向量替换掉目标向量。
种群中所有成成员必须要当作目标向量进行一次这样的操作，以便在下一代中出现相同个数的竞争者。在进化过程中，对每一代的向量都进行评价，记录最小化过程。

这种利用随机偏差扰动产生新个体的方式，可以获得一个收敛性非常好的结果，引导搜索过程向全局最优解逼近。

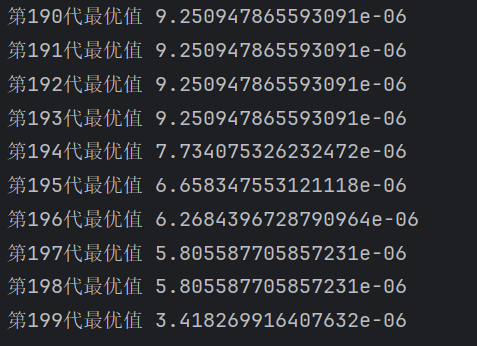
二、算法具体流程

整体流程

  1. 初始化
  2. 变异
  3. 交叉
  4. 选择
  5. 边界条件处理、

算法流程图如下：

初始化

初始化就是给种群中的每个个体的每个维度进行一个赋值，实现一个初始化的操作。每个个体表示如下：

其中，$i$ 表示个体在种群中的编号，$G$ 表示进化代数，$NP$ 代表种群规模。在差分进化算法中，一般假定所有随机初始化种群均符合均匀分布。设个体 $x_{i,G}$ 第 $j$ 维的界限为:

所有个体通过下式生产：

其中 $rand[0,1]$ 表示在 $[0,1]$ 之间的实数。当然，均匀产生随机数只是一种可能，如果可以预先知道解的概率分布，就不需要均匀产生，可以通过其分布规律，产生涵盖更多信息的解，进而提高重建效果。

变异

产生完初始种群后，进行变异操作，对于每个目标 $x_{i,G}(i=1,2,…,N P)$ 基本差分进化算法的变异向量产生方式如下：

其中，要求随机选择的个体序号 $r_{1}\,,r_{2}\,,r_{3}$ 互不相同，且与目标向量序号 $i$ 也不能相同，所以必须满足 $N P>4$ ；
变异算子 $F\in[0,2]$ 是一个实常数因数，它控制偏差变量的缩放。

交叉

这一步进行变异向量和目标向量的总体交叉。为了增加干扰参数向量的多样性，引入交叉操作，测试向量变为：

其中, $randb(j)$ 表示产生 $[0,1]$ 之间的随机数发生器的第j个估计值。$rnbr(i)\in\left(1,2,\ldots,D\right)$ 示一个随机选择的序列。，用它来确保 $u_{1_{i},G+1}$ 至少从 $v_{1_{i},G+1}$ 获得一个参数; $CR$ 表示交叉算子（表示一个概率），其取值范围为 $[0,1]$ 。

选择

经过上面的变异、交叉操作，差分进化算法按照贪婪准则将试验向量与当前种群中的目标向量 $x_{i,G}$ 进行比较，在下一代中，如果目标向量好，就选择目标向量，如果试验向量好，就选择试验向量。值得注意的实，试验向量只与目标向量进行个体比较，而不是现有种群中的所有个体（锦标赛选择）。

边界条件的处理

如果在变异过程中，我们编译出了可行域外的解， 即 $u_{ji,G+1}< x_{j}^{L}$ 或 $u_{j i,G+1}>x_{j}^{U}$ 那么

相关参数

种群数量 NP

$NP$ 越大，说明个体越多，种群多样性越好，寻优能力也越强，但同时也增加了计算难度。所以 $NP$ 不能无限取大。一般取 $5 D ≤ N P ≤ 10 D$ 之间，必须满足的是 $N P ≥ 4$，因为只有 $NP$ 大于4，才能有空间进行变异和杂交。

变异算子 F

变异算子 $F ∈ [ 0 , 2 ]$ 是一个实常数因数，它决定偏差向量的放大比例。

  • 如果太小，容易“早熟”，即陷入局部最优解。
  • 如果太大，不容易“收敛”。当 $F > 1$ 的时候，算法收敛到最优值变得十分困难，因为差分向量的扰动已经大于两个个体之间的距离了。

目前研究表面标明，$F$ 小于 $0.4$ 和 $F$ 大于 $1$ 的值仅偶尔有效，通常，$F = 0.5$ 是一个较好的初始选择。如果种群收敛过早，那么应该增大 $F$ 或 $NP$。

交叉算子 CR

一个 $[0,1]$ 之间的数，它控制着试验向量参数来自于随机选择的目标向量，还是变异向量。$CR$ 越大，发生交叉的可能性就越大，$CR$ 的一个较好的选择实 $0.1$，但较大的 $CR$ 通常会加速收敛。可以先尝试 $CR = 0.9$ 或 $CR=1.0$，查看是否可以快速产生一个快速解。

最大进化代数 G

最大进化代数 $G$ 表示差分进化算法运行结束的一个参数，最多更新 $G$ 代后就结束了，并将当前群体中最佳个体作为最优解输出。一般，$100 ≤ G ≤ 500$ 。

终止条件

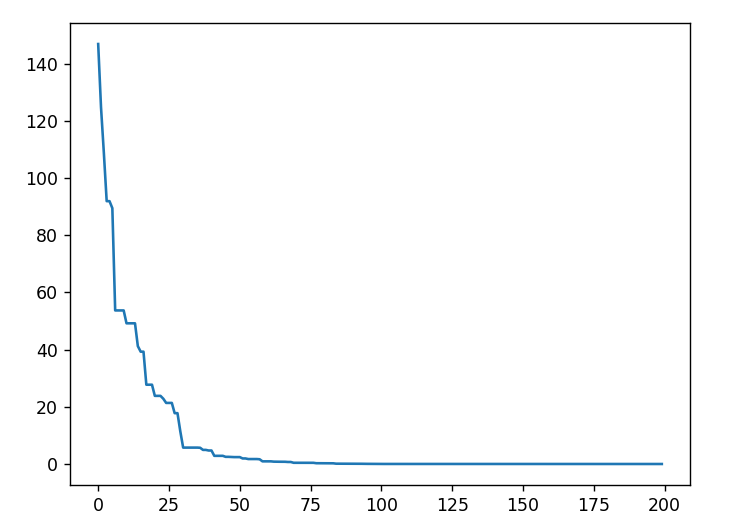
除最大进化代数可作为差分进化算法的终止条件外，还可以增加其他判定准则。一般当目标函数值小于阈值时程序终止，阈值常选为 $10^{-6}$ 。

三、一些改进方法

变异算子 F

对于变异算子 $F$ 的设置，可以采用如下模型：

其中 $G_m$ 是最大迭代次数， $G$ 是当前迭代次数。这个模型的好处是，在初期 $F$ 具有较大值为 $2F_0$ ，可以保持个体多样性，避免早熟，在后期变异率接近 $F_0$ 保留优良信息，避免最优解遭到破坏，增加全局最优解的概率。

变异算子 F

还可以设计随机范围的交叉算子，比如 $CR:0.5×[1+rand(0,1)]$ ，这样交叉算子的平均值维持在 $0.75$ 附近，考虑到了差分向量放大中可能的随机变化，有助于在搜索过程中保持群体多样性。

四、Python 代码

  • 解函数 $f(x)=\sum_{i=1}^{n}x_{i}^{2}\left(-20\leq x_{i}\ \leq20\right)$ 的最小值，其中个体 $x$ 的维数 $n=10$ 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
import numpy as np  
import matplotlib.pyplot as plt  
  
  
class DE(object):  
    def __init__(self, param_de):  
        self.NP = param_de['NP']  
        self.size = param_de['size']  
        self.xMin = param_de['xMin']  
        self.xMax = param_de['xMax']  
        self.F = param_de['F']  
        self.CR = param_de['CR']  
        self.pop_mut = None  
        self.pop_cro = None  
        self.best_archive = []  
  
    def pop_init(self):  
        pop_de = self.xMin + np.random.uniform(0, 1, (self.NP, self.size)) * (self.xMin - self.xMax)  
        return pop_de  
  
    @staticmethod  
    def calfitness(pop_de):  
        res = fan(pop_de)  
        return res  
  
    def mutation(self, pop_de, f_de):  
        self.pop_mut = np.zeros((self.NP, self.size))  
        for i in range(self.NP):  
            index = np.arange(self.NP)  
            index = np.delete(index, i)  
            r1, r2, r3 = pop_de[np.random.choice(index, 3, replace=False)]  
            self.pop_mut[i] = r1 + f_de * (r2 - r3)  
        return self.pop_mut  
  
    def crossover(self, pop_de):
        self.pop_cro = pop_de.copy()
        for i in range(self.NP):
            rn = np.random.randint(0, self.size, 1)
            rand = np.random.uniform(0, 1, self.size)
            self.pop_cro[i, rn] = self.pop_mut[i, rn]
            condition = (rand <= self.CR)
            self.pop_cro[i] = np.where(condition, self.pop_mut[i], self.pop_cro[i])
        return self.pop_cro
  
    def check_bound(self):  
        for i in range(self.NP):  
            for j in range(self.size):  
                condition = (self.pop_cro[i, j] < self.xMin) or (self.pop_cro[i, j] > self.xMax)  
                if condition:  
                    self.pop_cro[i, j] = self.xMin + np.random.uniform(0, 1, 1) * (self.xMax - self.xMin)  
        return self.pop_cro  
  
    def selection(self, pop_de, fit):  
        pop_c = self.check_bound()  
        fit_c = self.calfitness(self.pop_cro)  
        condition = fit_c < fit  
        fit[condition] = fit_c[condition]  
        pop_de[condition] = pop_c[condition]  
        index = np.argsort(fit.flatten())  
        best_de = fit[index[0]]  
        self.best_archive.append(best_de)  
        return pop_de, fit, best_de  
  
  
def fan(pop_f):  
    res = np.sum(pop_f**2, axis=1)  
    return res  
  
  
if __name__ == '__main__':  
    param = {  
        'NP': 100,  
        'size': 10,  
        'xMin': -10,  
        'xMax': 10,  
        'F': 0.5,  
        'CR': 0.8,  
        'G': 200  
    }  
    G = param['G']  
    F = param['F']  
    de = DE(param)  
    pop = de.pop_init()  
    fitness = de.calfitness(pop)  
    for gen in range(G):  
        lamda = np.exp(1 - G / (G + 1 - gen))  
        f = F * np.power(2, lamda)  
        de.mutation(pop, f)  
        de.crossover(pop)  
        pop, fitness, best = de.selection(pop, fitness)  
        print(f"第{gen}代最优值", best)  
    plt.figure()  
    plot_x = np.arange(G)  
    plot_y = de.best_archive  
    plt.plot(plot_x, plot_y)  
    plt.show()

结果